BP 误差反向传播法数学知识 - online
BP 误差反向传播法数学知识
前言
在学习李宏毅老师的机器学学习的前两节课的时候,学到了关于机器学习的多层感知机的知识,也就是深度学习,想到了前面学习的BP误差反向传播我没理解其中的数学办法,于是有了这篇笔记
反向传播算法
我们知道其实多层感知机算法也就是通过构造函数,然后算构造函数得到的预期值和实际值的差值去不断优化函数,直到找到一个函数能够去最好的处理这个问题,也是就李宏毅老师说的,深度学习其实就是looking for Function
构造函数
在前面学习linear model的时候(也就是线性模型)我们寻找的函数是$y=b+ax_1$这种,但是由于无论我构建多少层这样的函数,最后的结果也只能是一个直线,我们实际上的模型中是需要线性和曲线的。
于是诞生出了Piecewise Linear model,我们可以通过下图来理解什么是piecewise Linear,我们可以通过将线1+线2+线3+线0+常量得到一个折线。
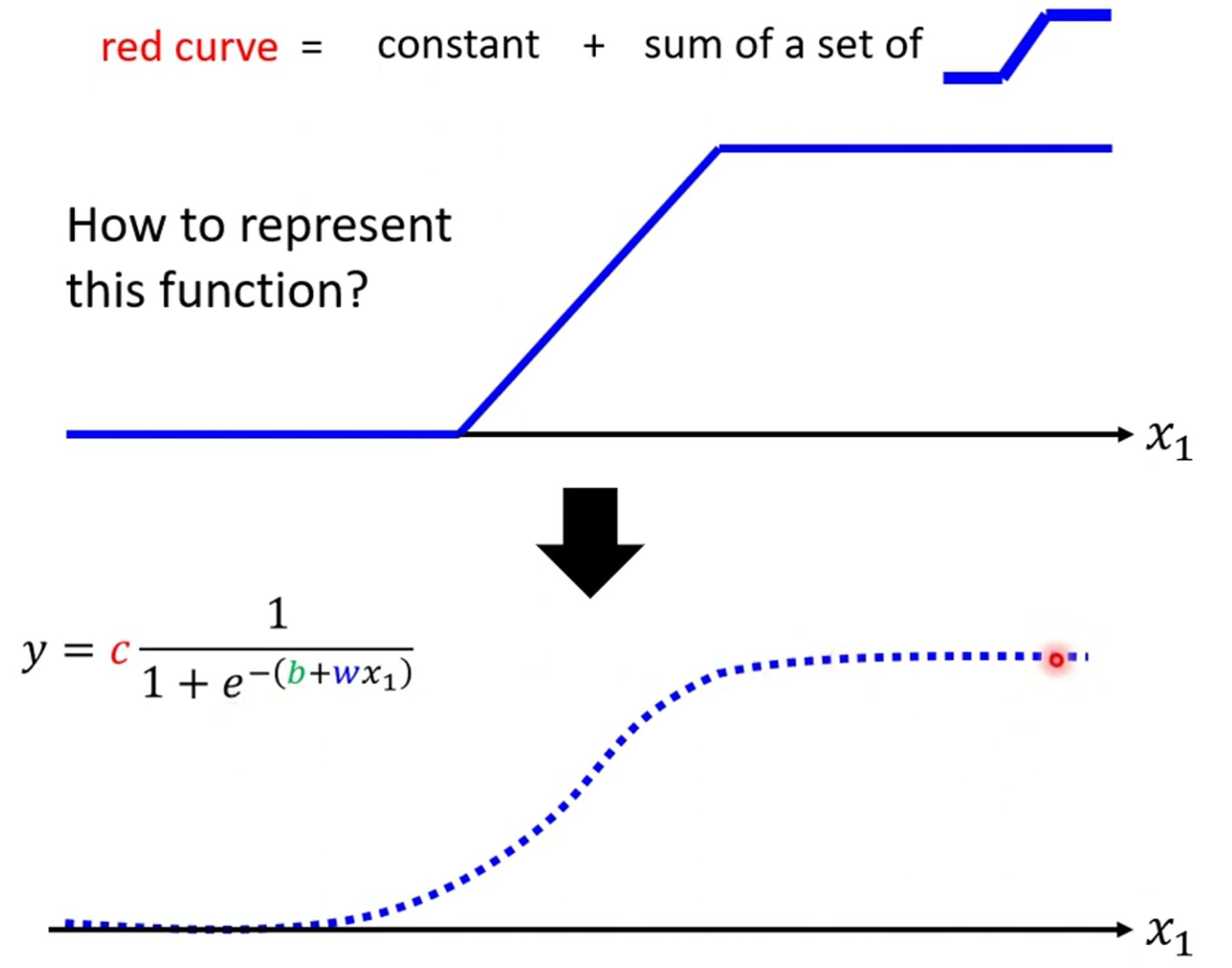
我们将形如线1,2,3的线称作RELU,我们还可以使用$y=c\frac{1}{1+e^{-(b+wx_1)}}$这样的算式来近似RELU,我们叫这样的函数为sigmoid,RELU也可以叫Hard sigmoid
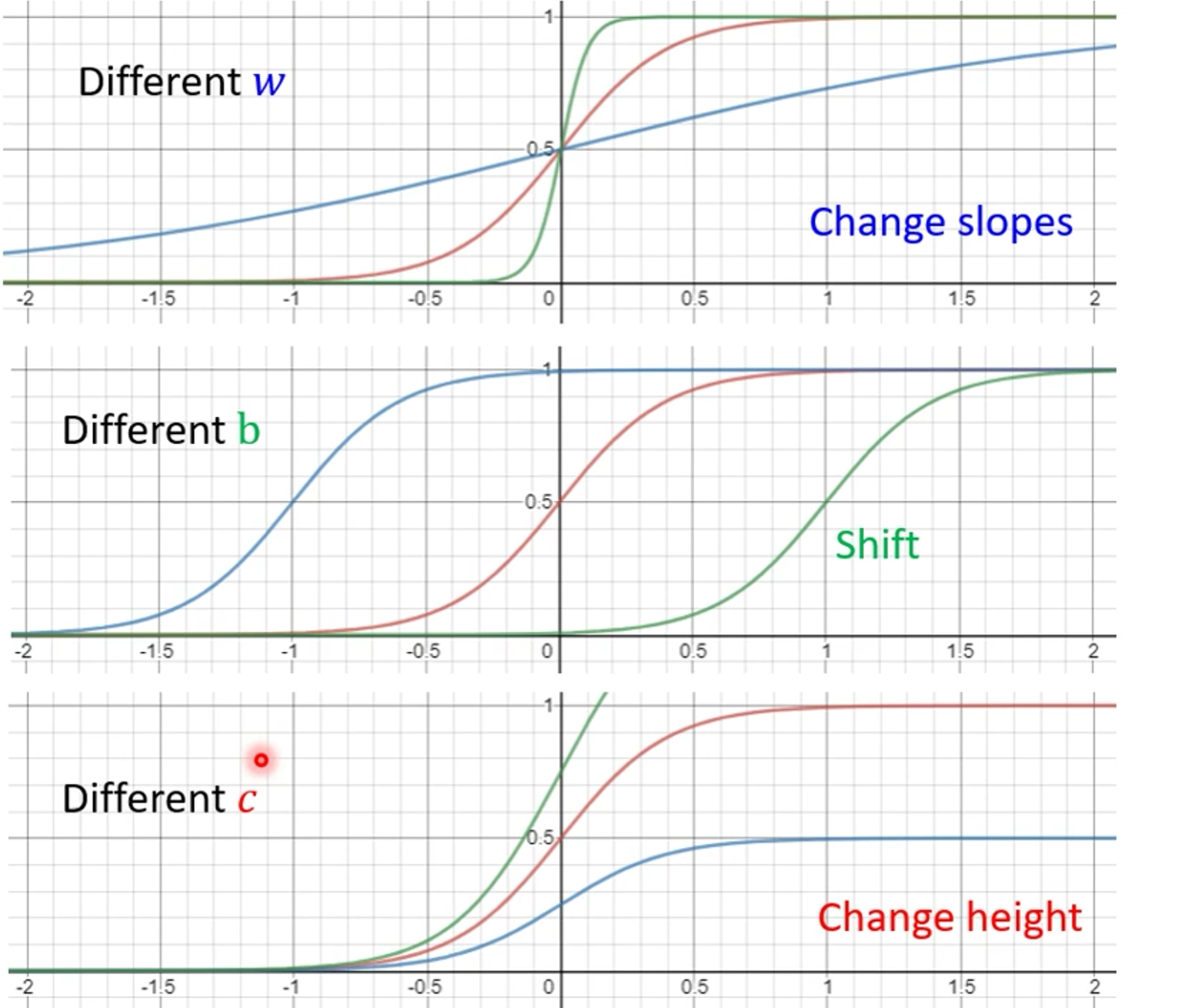
后面我们会基于sigmoid来进行讨论,我们改变c,b,w会改变sigmoid的不同的值
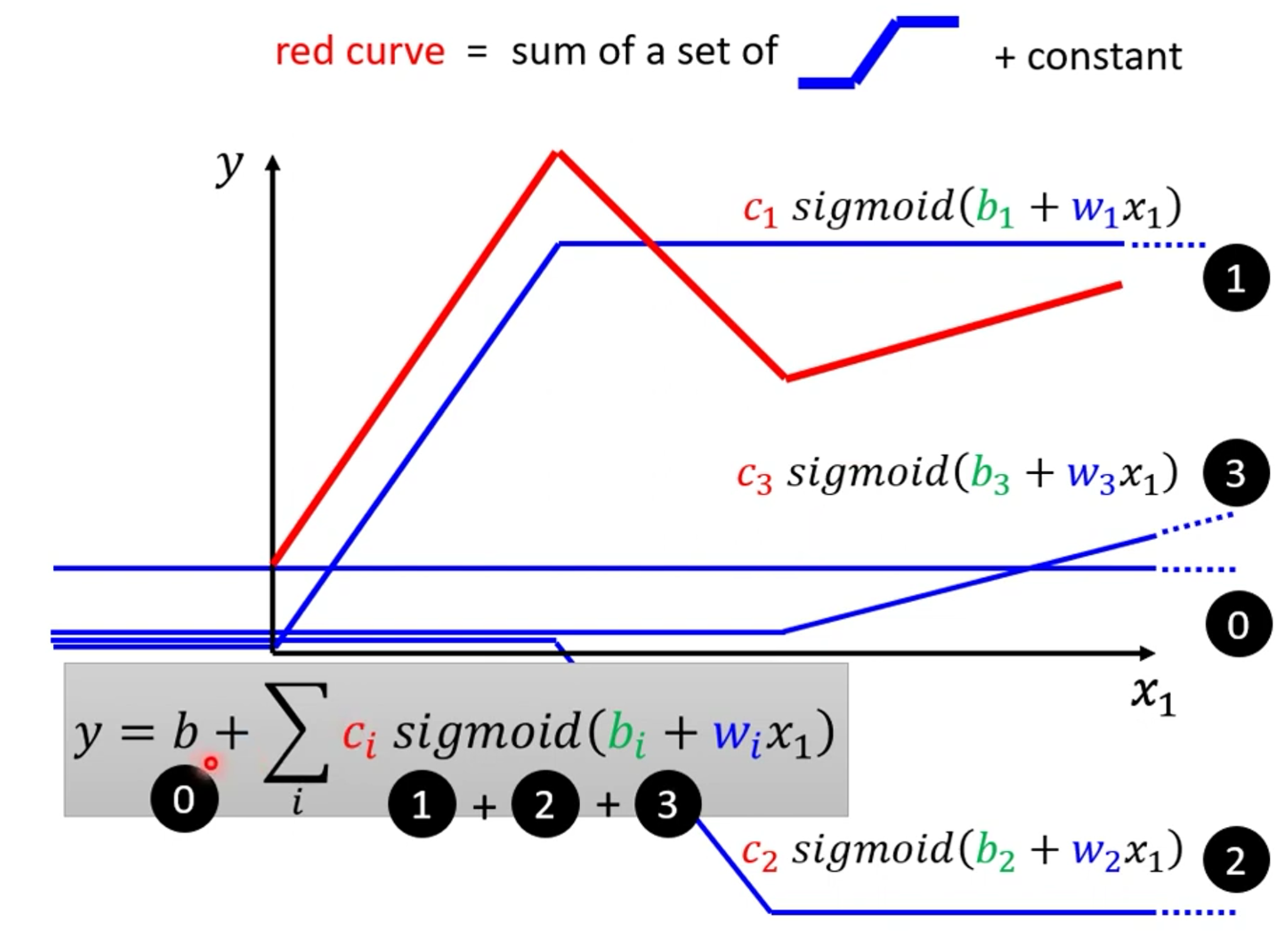
现在我们就可以把上面的用RELU表示的折线表示为sigmoid表示的,如下
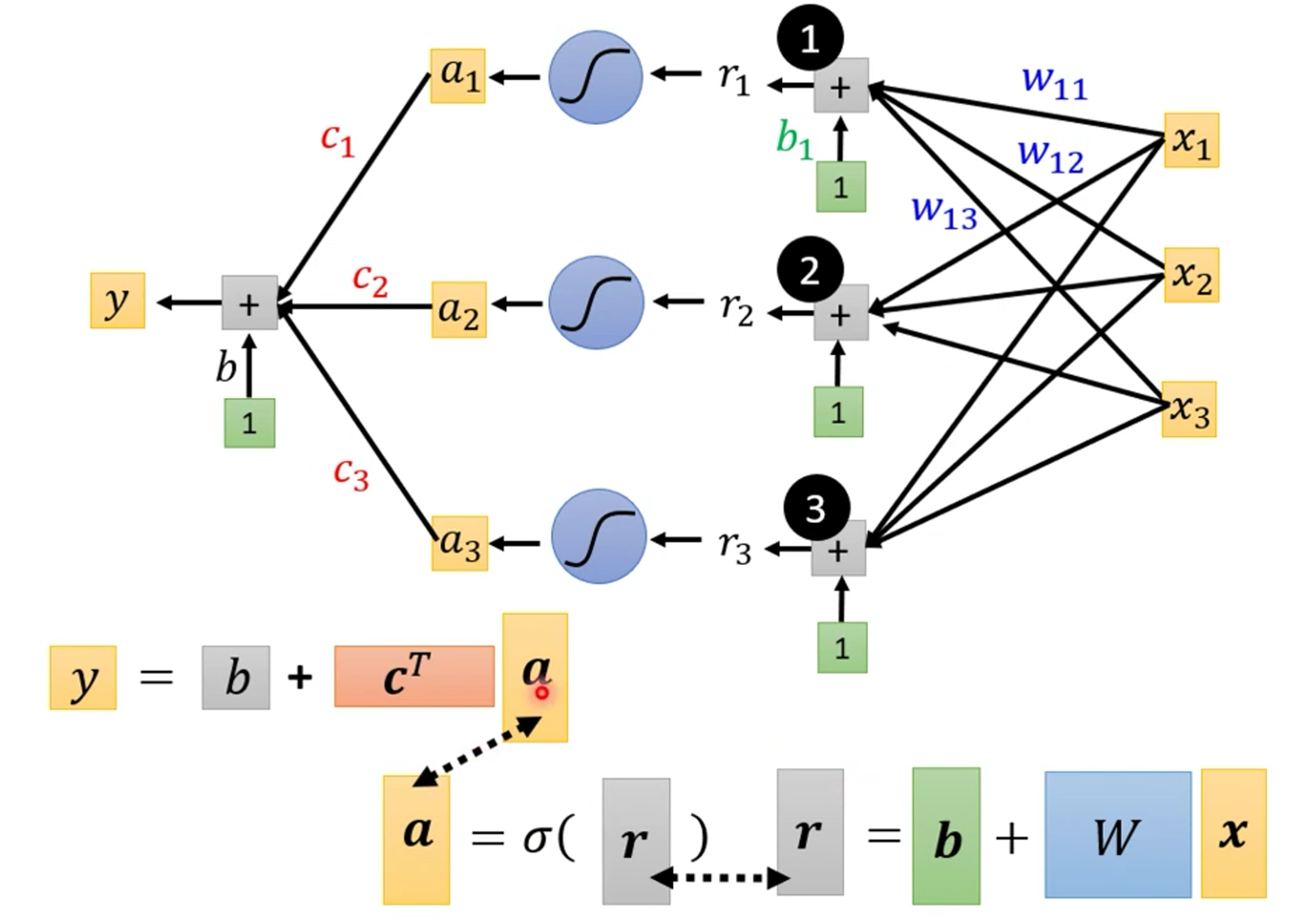
我们就可以得出函数$y=b+\sum_{i}^{n}{C_i}sigmoid(b_i+w_iX_1)$表示新的折线了,然后我们用图进行理解为什么是这个公式
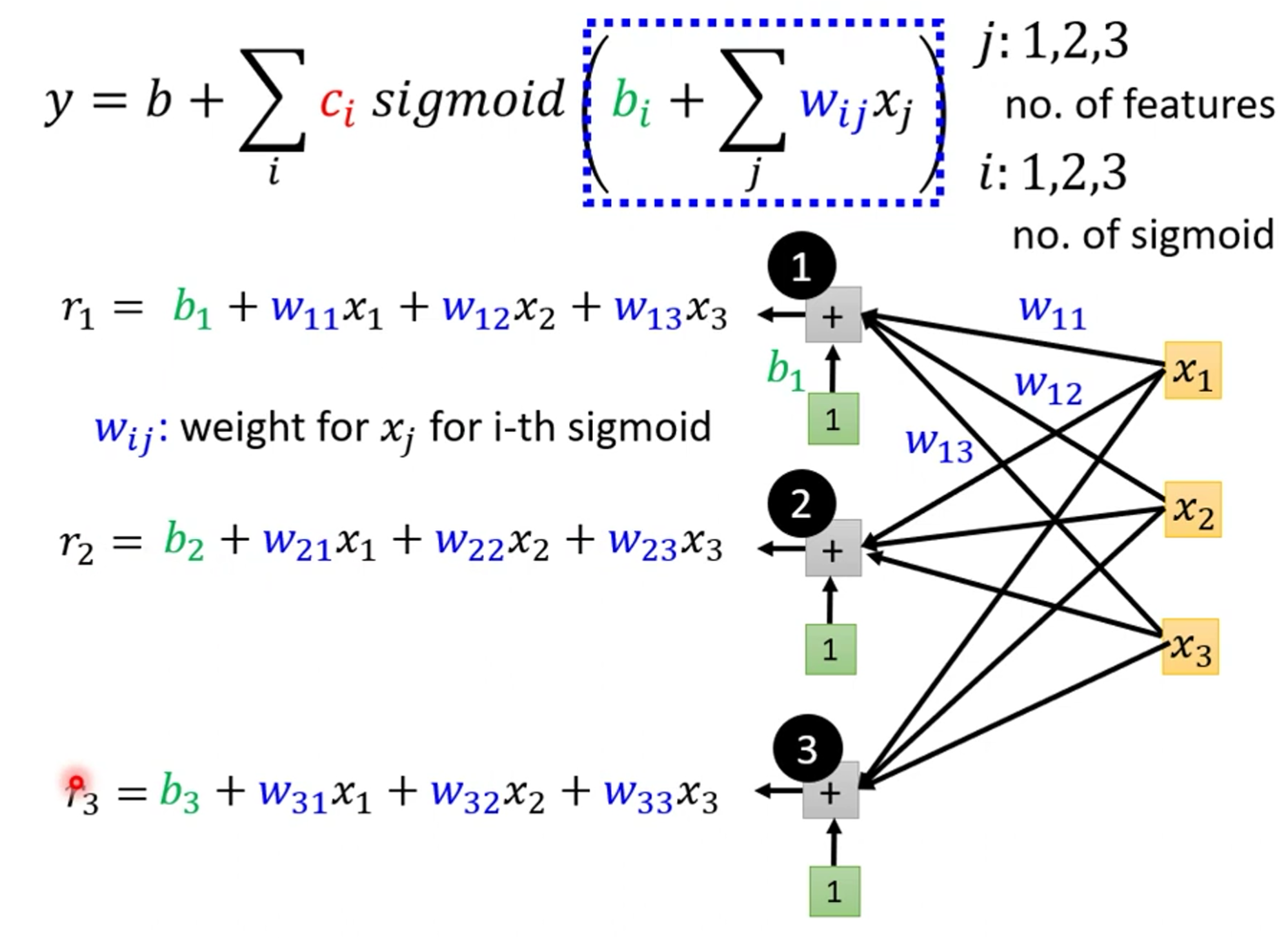
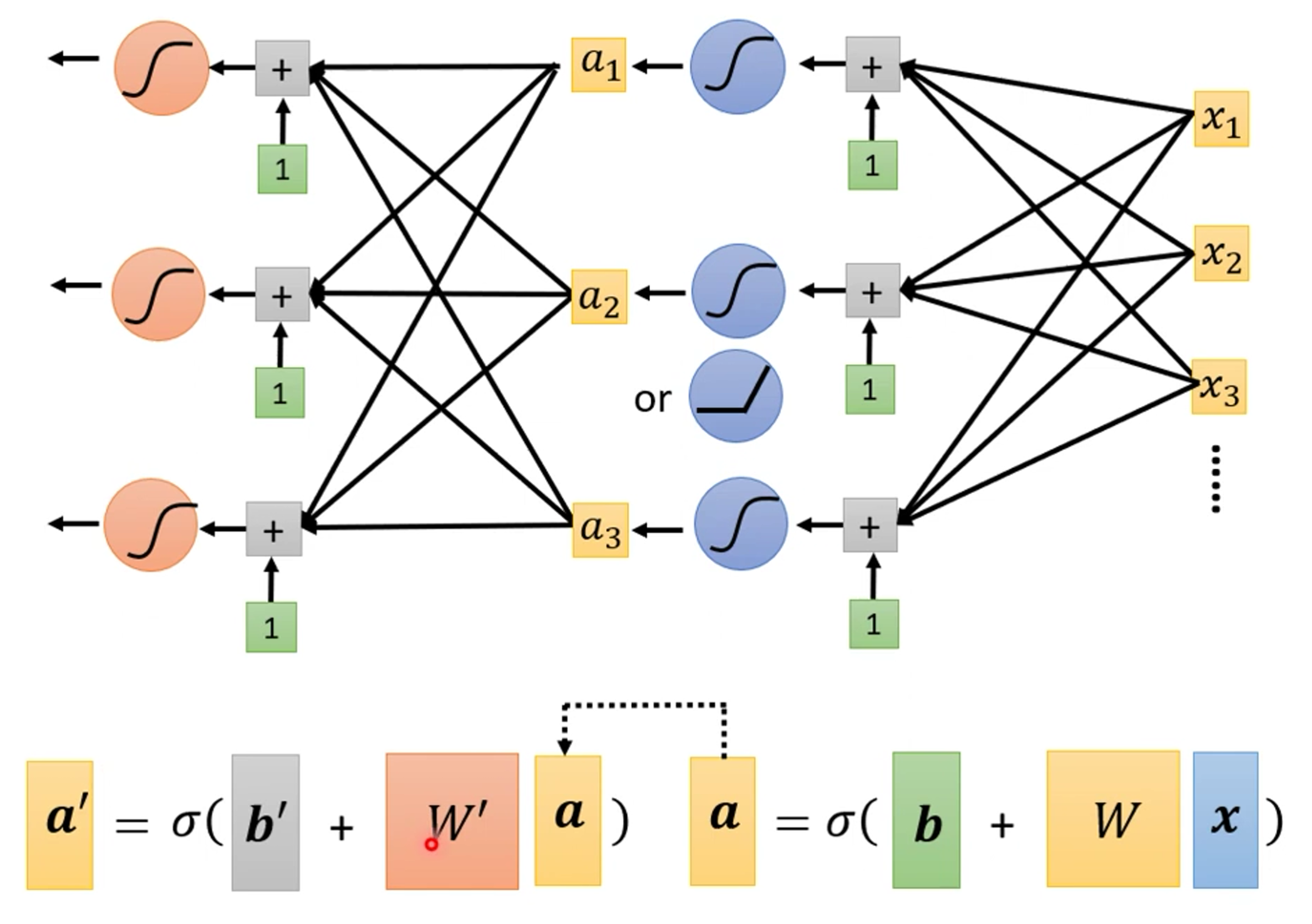
然后我们再进行简化一下这个函数为矩阵表示
然后我们用一个希腊字符表示sigmoid,然后函数可以表示为下图
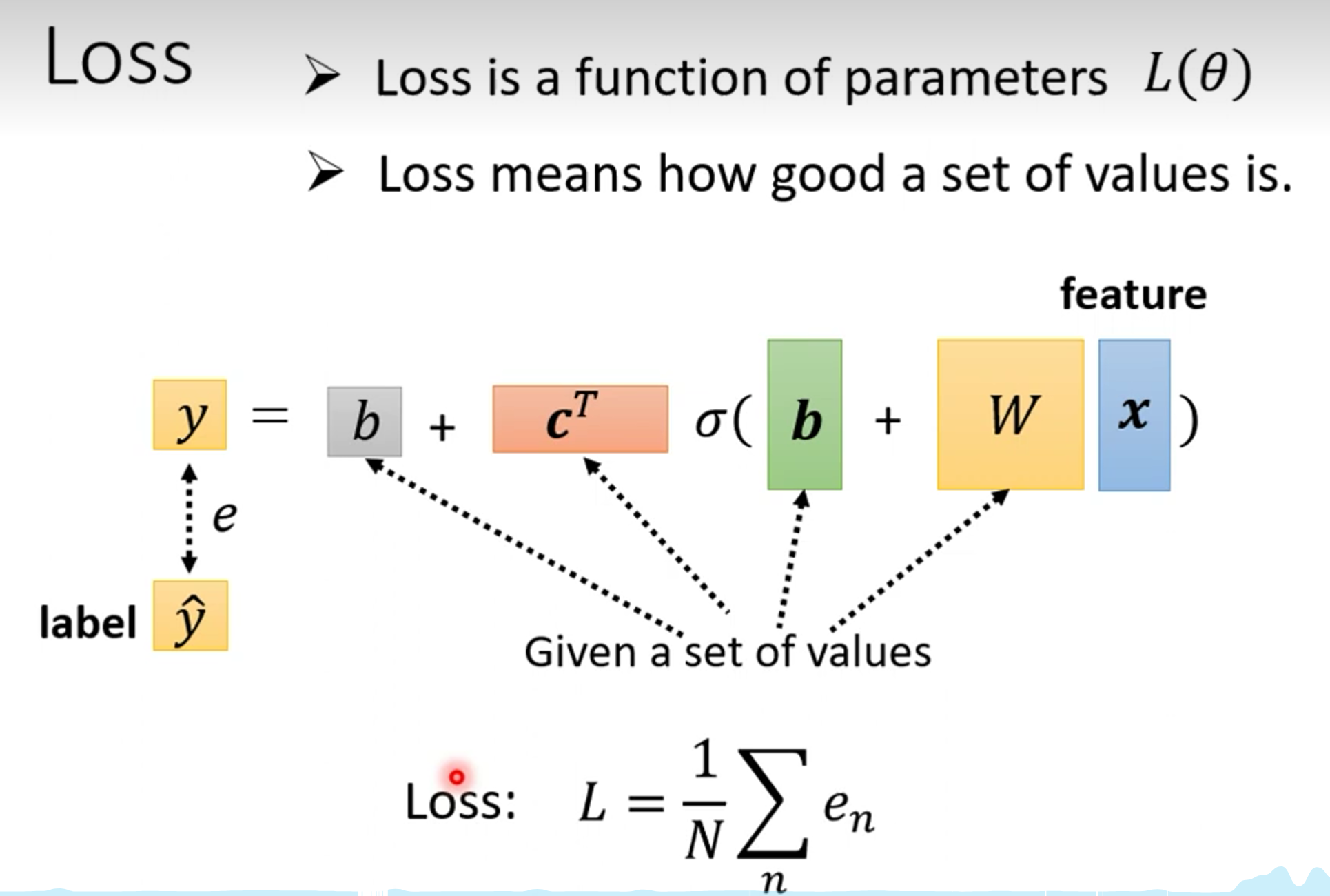
函数反馈修改参数
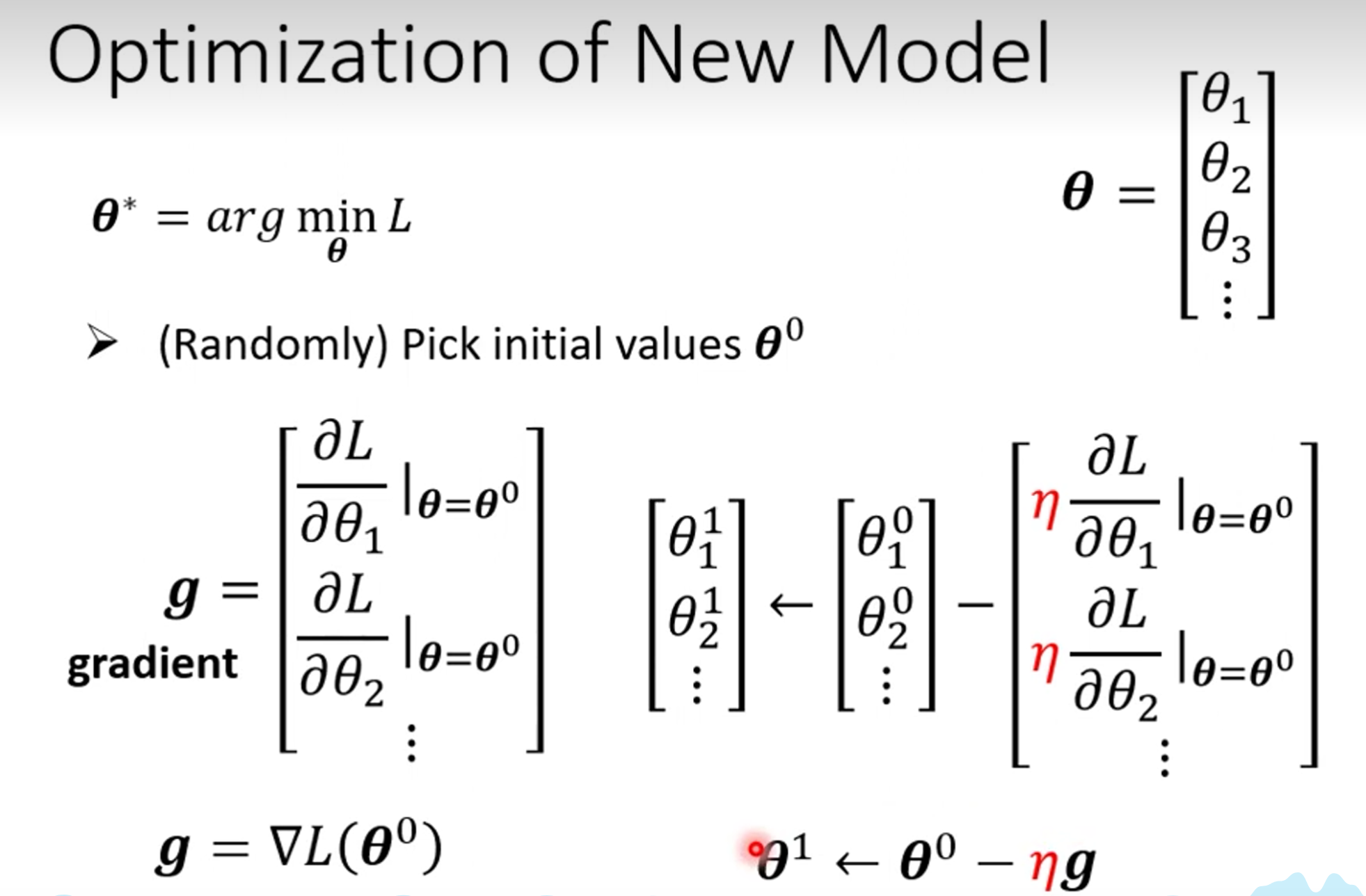
我们前面定义了函数,并且能够产生折线函数了,现在我们来写函数的反馈方法,和线性的反馈算法是一样的
这里的$\theta$表示的是参数,也就是$b_1,b_2,w$这些参数,反馈算法如下,也就是将几个$\frac{∂L}{∂\theta_1}|_{\theta=\theta^0}$算出来然后,矩阵相减即可
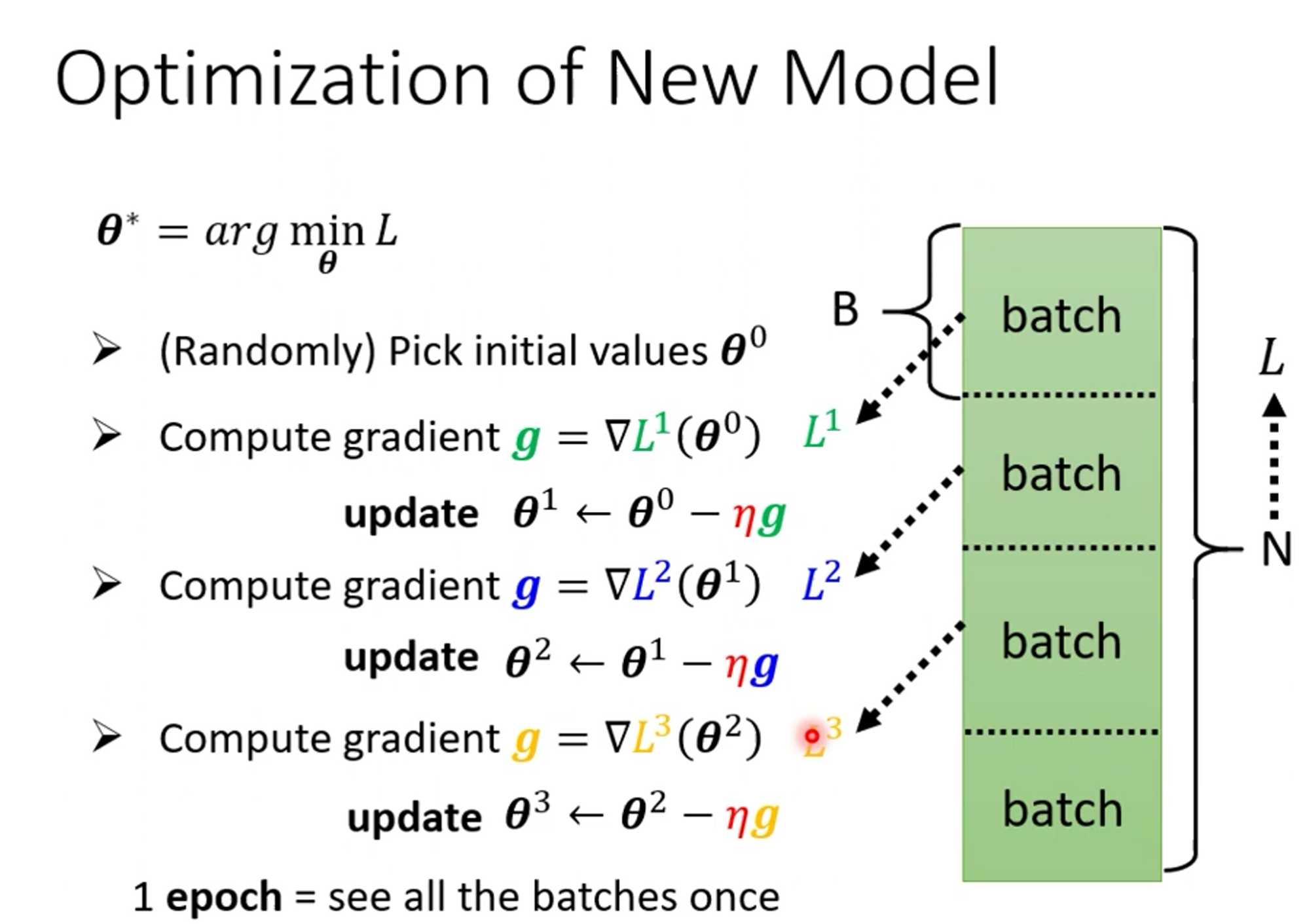
然后我们需要对训练资源进行分组,然后分组进行更新,也就是说如果有10000个资源,我们10个为1组,就能更新1000次,更新一次我们叫一次update,所以资源都训练完了叫一次epoch
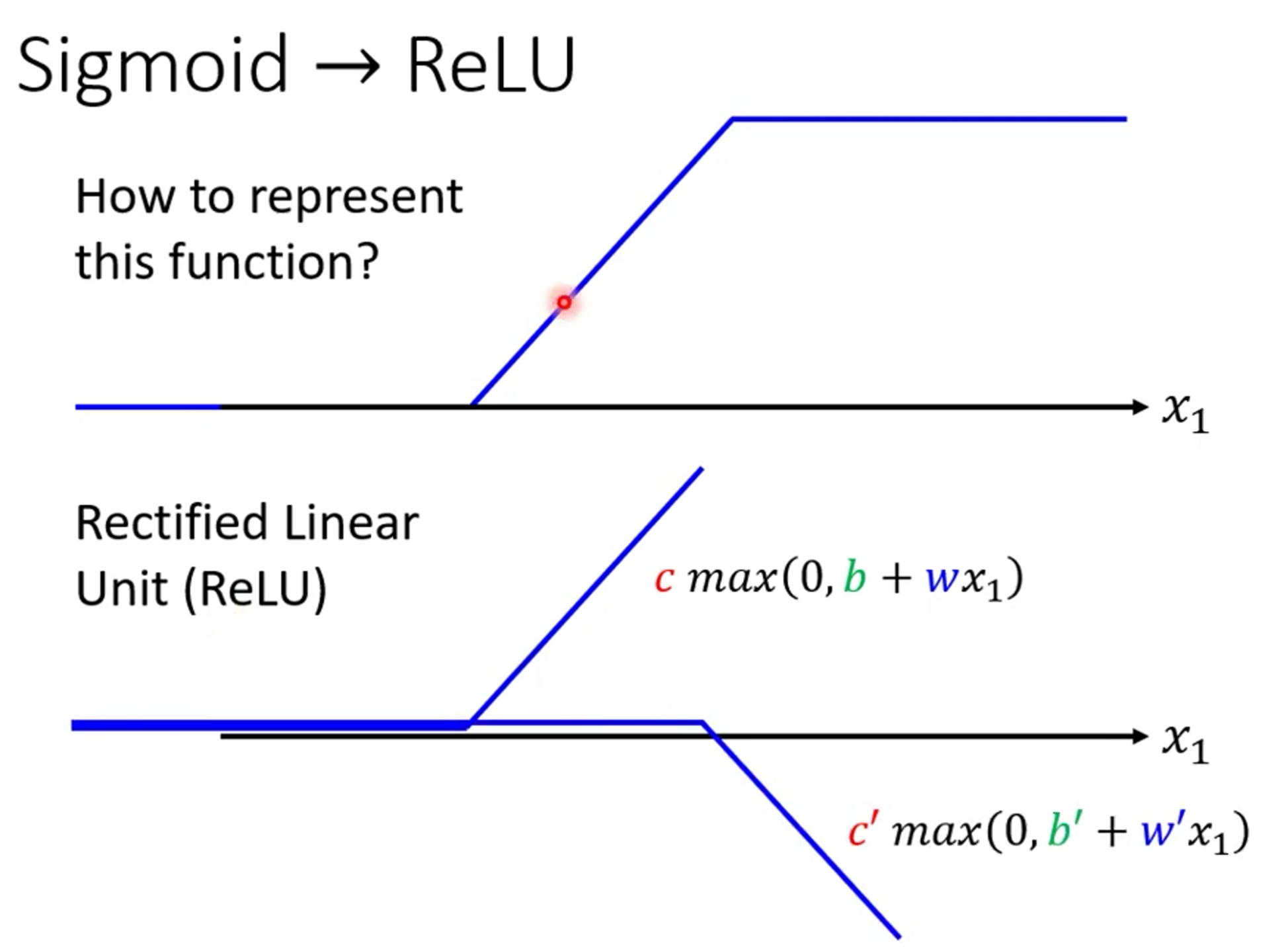
前面我们学了sigmoid的数学表示,但是我们没有学RELU的数学表示,RELU的数学表示为$y=c*max(0,b+wx_1)$,如下图
对比一下RELU和sigmoid,由于RELU需要两条去表示,这里需要用2i
在我们写代码的时候一般是用的RELU,当然都可以使用,而且我们在可以不止一次的进行RELU和Sigmoid我们可以多次进行使用,这也就是为什么叫多层感知机的原因。