大语言模型的涌现能力:现象与解释
大语言模型的涌现能力:现象与解释
前言
在学习大语言模型的时候,接触到了大佬的分享,前沿的知识,感觉很有帮助,特此记录,只是简单记录,文章来源会在后面的参考资料标注出来
问答
注释1:有人问了,既然很多自然现象也体现出涌现能力,那么大语言模型的涌现现象需要解释吗?我个人认为是需要的。毕竟,说大语言模型的某个特殊现象属于“涌现现象”,也是被个别研究提出来,未有确切证明或证据,是否它和自然现象中出现的涌现现象内在机制是类似或一样的,其实可以存疑。而且我认为大模型的这个现象,背后应该有些我们可以理解的原因。如果我们不追求现象背后的解释,仅仅把目前解释不了的现象统一归类为涌现或者其它什么概念,就此了之。那么,其实我们也可以把大模型的目前理解不了的很多现象,统一归类为这是一种“神迹”,那世界上很多事情就简单多了。另另,用Grokking解释涌现现象,尽管我把它称为”用玄学解释玄学“,但是觉得还是值得深入探索的方向,也许可以把上面的说法,优化为”用含玄量较低的玄学解释另外一个含玄量较高的玄学“。
注释2:如果仔细分析的话,大语言模型的这个所谓“涌现现象”,如果仅仅把现象归因于模型规模,目前看大概率是把问题简化了,很有可能影响因素是多样化的。如果让我归纳的话,某个任务,大语言模型是否会出现“涌现现象” ,很可能是以下多因素影响的某个未知函数:
(模型参数规模,训练数据量大小,训练充分程度,具体任务类型)
什么是大模型的涌现能力
复杂系统学科里已经对涌现现象做过很久的相关研究。那么,什么是“涌现现象”?当一个复杂系统由很多微小个体构成,这些微小个体凑到一起,相互作用,当数量足够多时,在宏观层面上展现出微观个体无法解释的特殊现象,就可以称之为“涌现现象”。
在日常生活中也有一些涌现现象,比如雪花的形成、堵车、动物迁徙、涡流形成等。这里以雪花为例来解释:雪花的构成是水分子,水分子很小,但是大量的水分子如果在外界温度条件变化的前提下相互作用,在宏观层面就会形成一个很规律、很对称、很美丽的雪花。
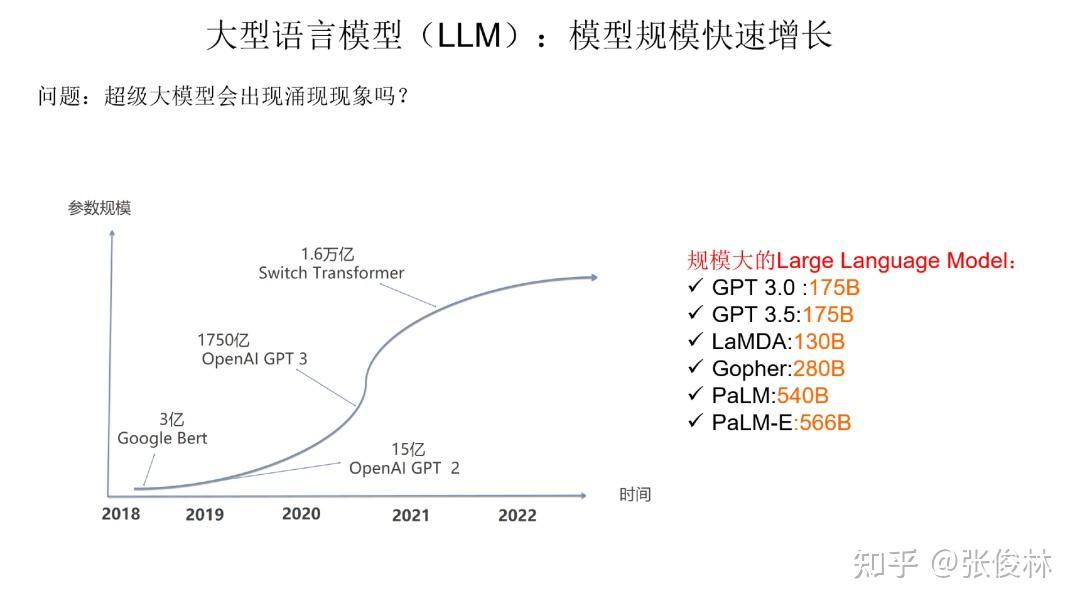
那么问题是:超级大模型会不会出现涌现现象?显然我们很多人都知道答案,答案是会的。
我们先来看下大语言模型的规模增长情况。如果归纳下大语言模型在近两年里最大的技术进展,很有可能就是模型规模的快速增长。如今,大规模模型一般超过 100B,即千亿参数。如 Google 发布的多模态具身视觉语言模型 PaLM-E,由540B 的 PaLM 文本模型和 22B 的 VIT图像模型构成,两者集成处理多模态信息,所以它的总模型规模是 566B。
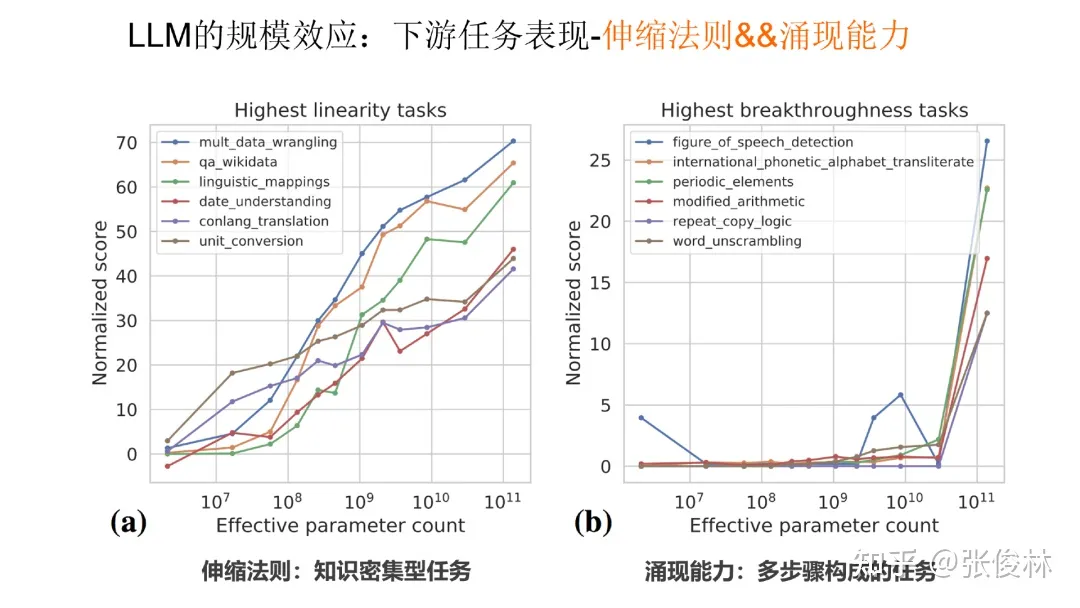
大语言模型规模不断增长时,对下游任务有什么影响?对于不同类型的任务,有三种不同的表现:
第一类任务表现出伸缩法则:这类任务一般是知识密集型任务。随着模型规模的不断增长,任务效果也持续增长,说明这类任务对大模型中知识蕴涵的数量要求较高。
第二类任务表现出涌现能力:这类任务一般是由多步骤构成的复杂任务。只有当模型规模大到一定程度时,效果才会急剧增长,在模型规模小于某个临界值之前,模型基本不具备任务解决能力。这就是典型的涌现能力的体现。这类任务呈现出一种共性:大多数是由多步骤构成的复杂任务。
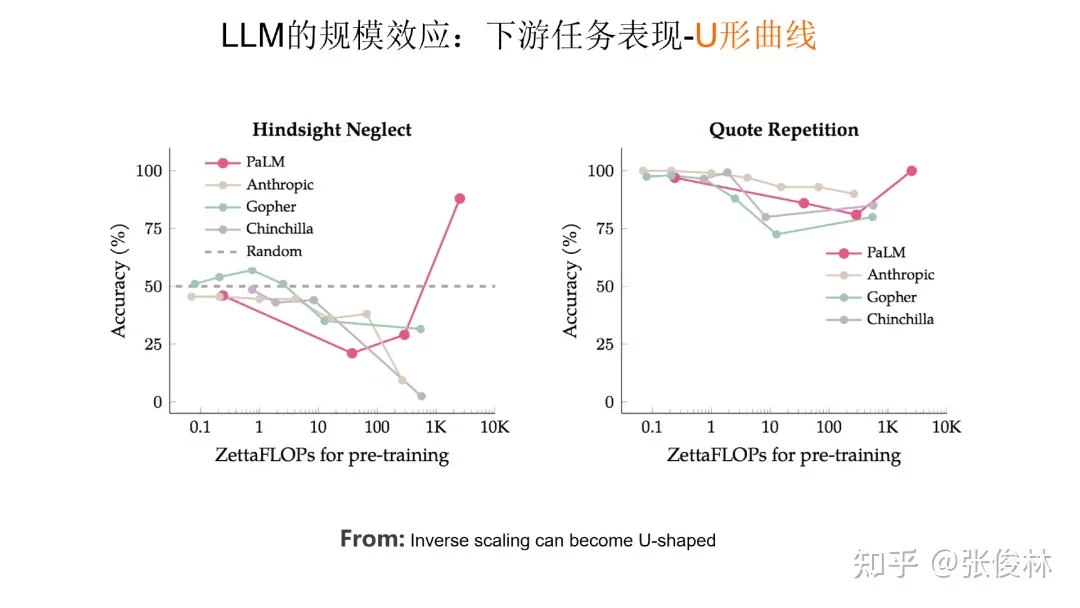
第三类任务数量较少,随着模型规模增长,任务效果体现出一个U 形曲线。如上图所示,随着模型规模增长,刚开始模型效果会呈下降趋势,但当模型规模足够大时,效果反而会提升。如果对这类任务使用 思维链CoT技术,这些任务的表现就会转化成伸缩法则,效果也会随着模型规模增长而持续上升。
因此,模型规模增长是必然趋势,当推进大模型规模不断增长的时候,涌现能力的出现会让任务的效果更加出色。
LLM 表现出的涌现现象
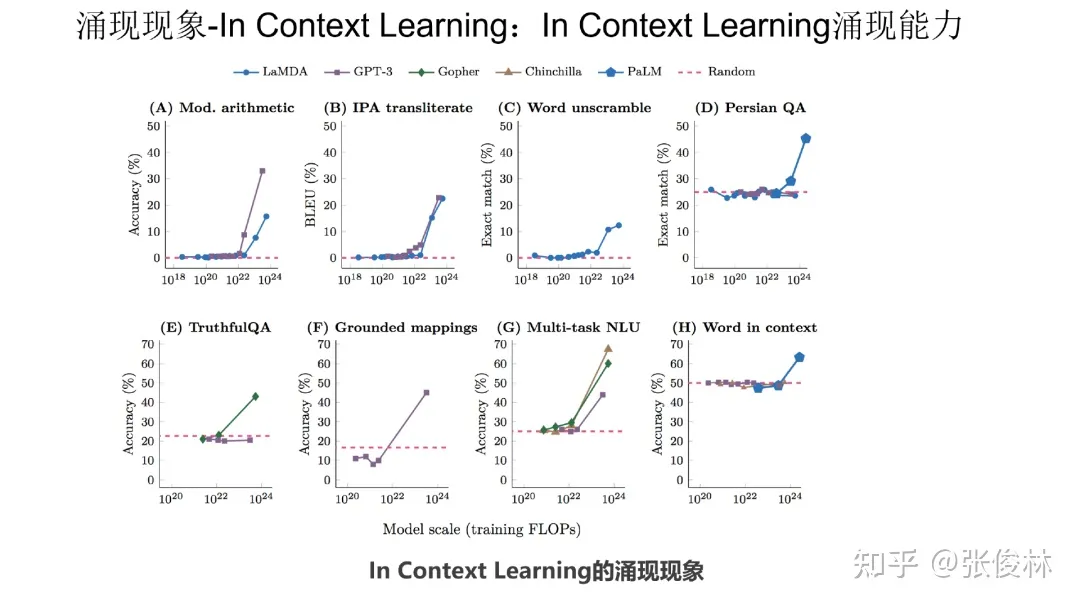
目前有两大类被认为具有涌现能力的任务,第一类是 In Context Learning(“Few-Shot Prompt”),用户给出几个例子,大模型不需要调整模型参数,就能够处理好任务(参考上图给出的情感计算的例子)。
如上图展示,利用In Context Learning,已经发现在各种类型的下游任务中,大语言模型都出现了涌现现象,体现在在模型规模不够大的时候,各种任务都处理不好,但是当跨过某个模型大小临界值的时候,大模型就突然能比较好地处理这些任务。
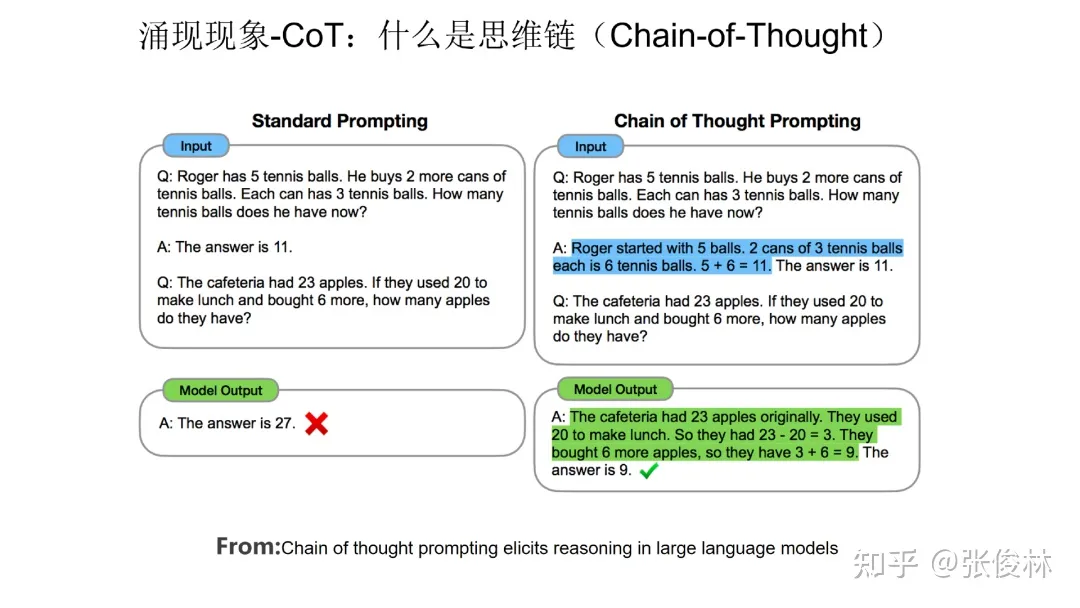
第二类具备涌现现象的技术是思维链( CoT)。CoT本质上是一种特殊的few shot prompt,就是说对于某个复杂的比如推理问题,用户把一步一步的推导过程写出来,并提供给大语言模型(如下图蓝色文字内容所示),这样大语言模型就能做一些相对复杂的推理任务。
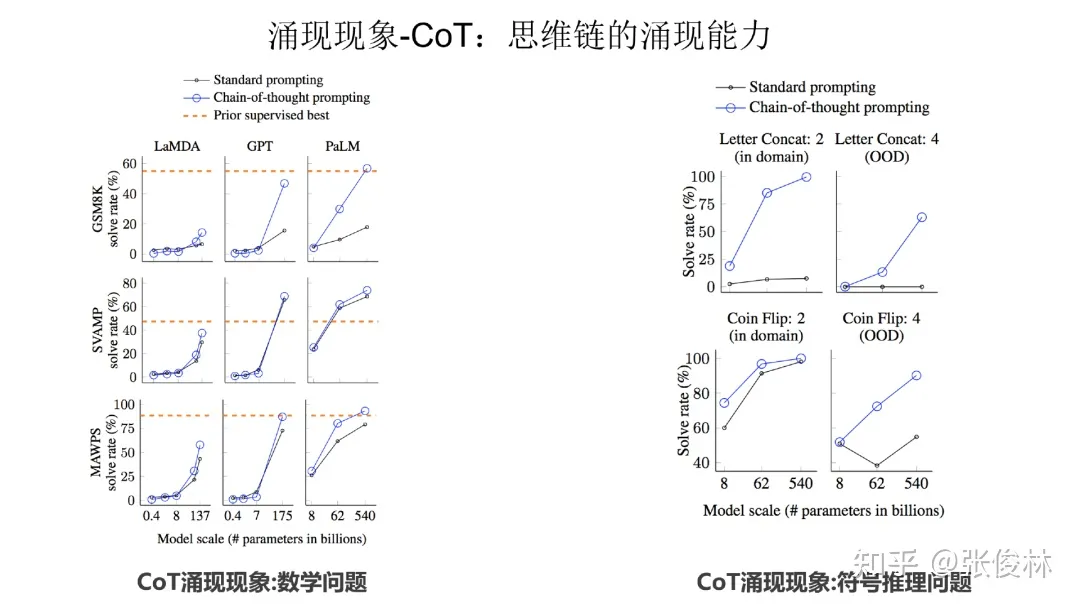
从上图可以看出,无论是数学问题、符号推理问题,CoT 都具备涌现能力。
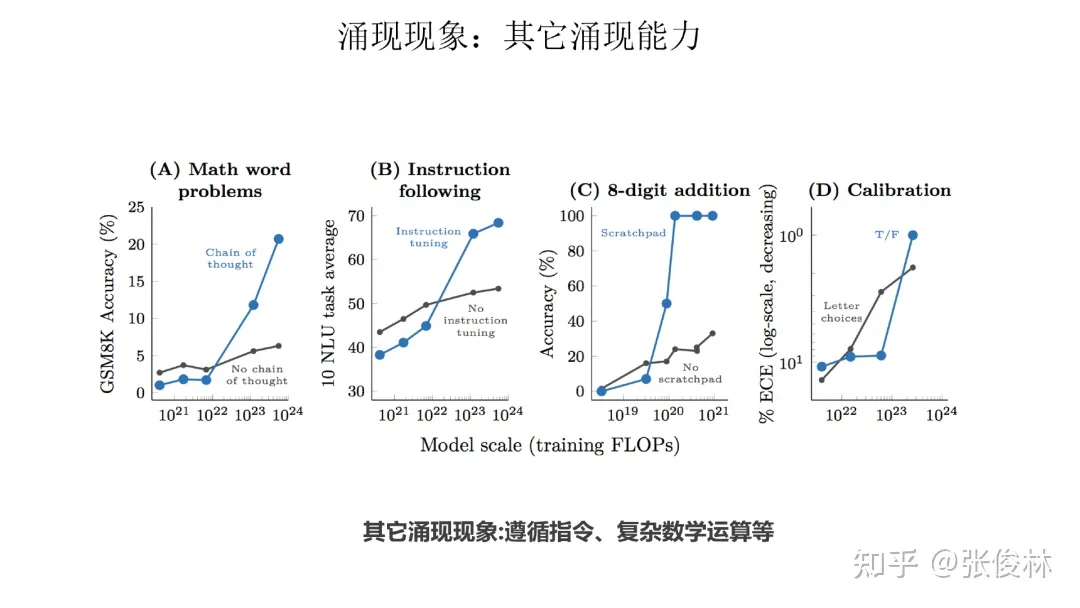
除此之外,其他任务也有涌现能力,如上图所示的数学多位数加法、命令理解等。
LLM 模型规模和涌现能力的关系
可以看出,涌现能力和模型的规模大小有一定的关联关系 ,那么,我们的问题是,具体而言,两者是怎样的关系呢?
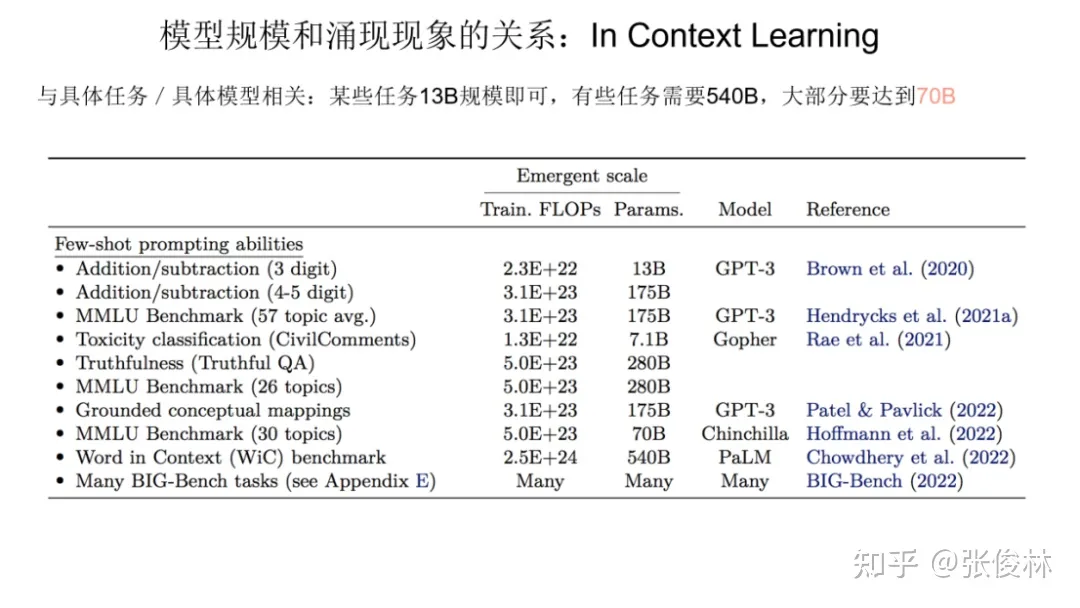
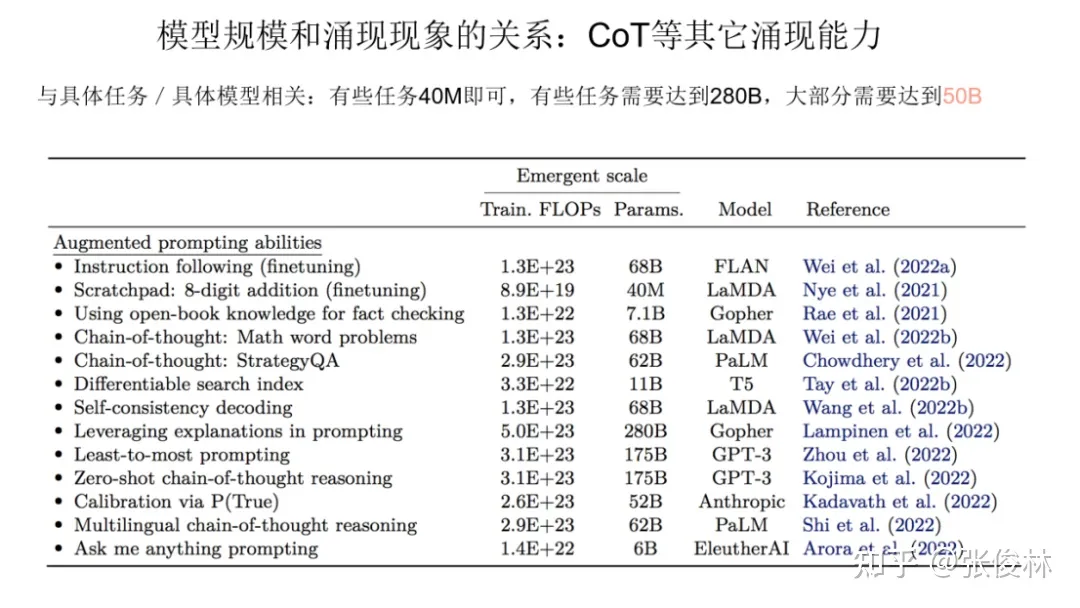
我们分头来看,先看下In Context Learning 的涌现能力和模型规模的关系。上图展示了对于不同类型的具体任务, In Context Learning 的涌现能力和模型规模的对照关系。
从图中数据可以看出,我们很难给出一个唯一的模型大小数值。不同类型的任务,在In Context Learning方面,模型多大才具备涌现能力,这跟具体的任务有一定的绑定关系。例如:图表第一行的3位数加法任务,模型只要达到 13B(130亿参数),就可以具备涌现能力,但是对倒数第二行的 Word in Context Benchmark任务而言,目前证明,只有540B 大小的模型才可以做到这点。我们只能说,就In Context Learning而言,如果模型达到 100B, 大多数任务可以具备涌现能力。
对于CoT来说,结论也是类似的,就是说要想出现涌现能力,模型规模大小和具体任务有一定的绑定关系。
把模型做小会影响 LLM 的涌现能力吗?
因为对很多任务来说,只有模型规模做到比较大,才能具备涌现能力,所以我个人比较关心下列问题:我们能不能把模型做小?把模型做小是否会影响到LLM的涌现能力?这是个很有趣的问题。我们这里拿两个小模型代表来探讨这个问题。
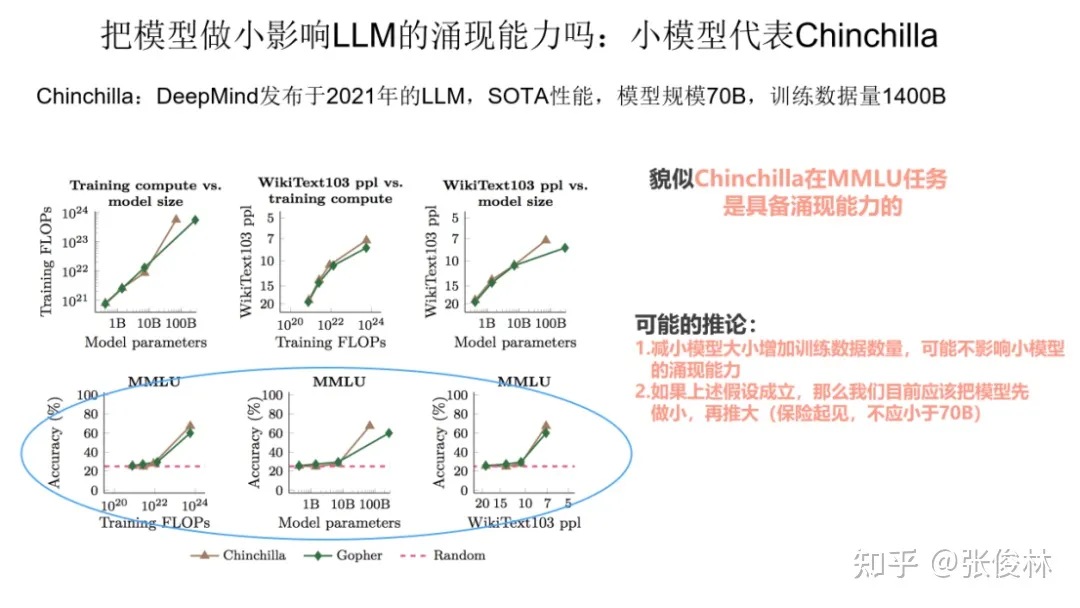
第一个小模型代表,是 DeepMind 2021年发表的模型 Chinchilla,这个模型目前做各种任务的效果,和 540B大小的PaLM 基本相当。Chinchilla的思路是给更多的数据,但是把模型规模做小。具体而言,它对标的是Gopher模型,Chinchilla模型大小只有 70B,是Gopher的四分之一,但是付出的代价是训练数据总量,是Gopher的四倍,所以基本思路是通过放大训练数据量,来缩小模型规模。
我们把Chinchilla规模做小了,问题是它还具备涌现能力吗?从上图给出的数据可以看出,起码我们可以说, Chinchilla 在自然语言处理的综合任务 MMLU 上是具备涌现能力的。如果小模型也能具备涌现能力,那么这其实侧面反映了一个问题:对于类似 GPT3 这样的模型而言,很可能它175B 这么多的模型参数,并没有被充分利用,因此,我们在以后训练模型的时候,可以考虑先增加训练数据,降低模型参数量,把模型做小,先把模型参数利用充分,在这个基础上,再继续增加数据,并推大模型规模。也即是说,目前看,我们先把模型做小,再把模型做大,看上去是可行的。
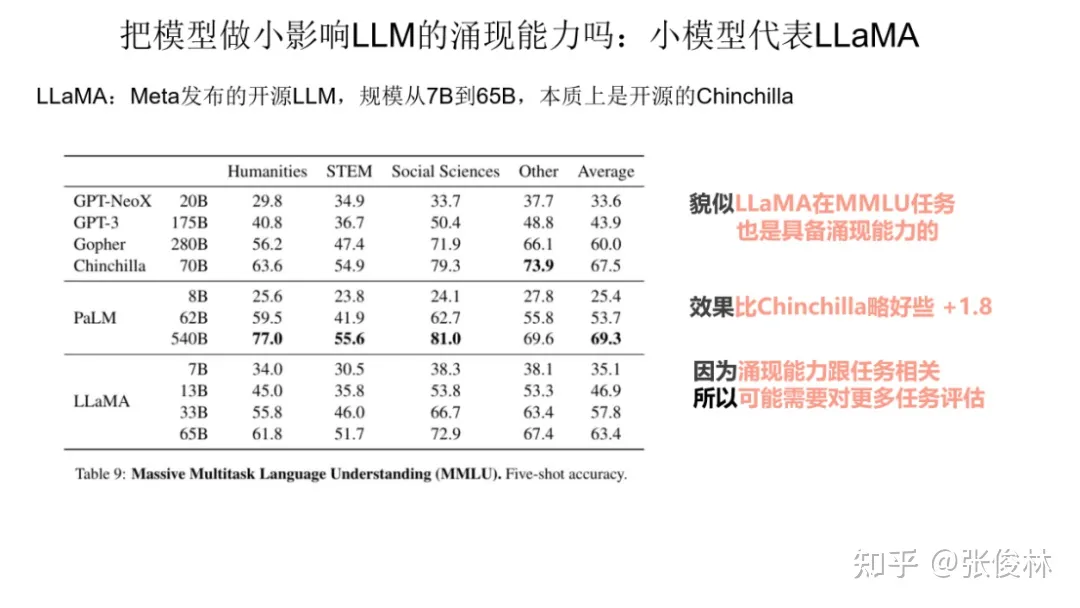
第二个小模型代表是 Meta 发布的开源模型 LLaMA,它的做法其实很好理解,本质上就是开源的 Chinchilla,它的思路是完全遵照 Chinchilla 来做的,就是说增加训练数据,但是把模型规模做小。那么LLaMA是否具备涌现能力呢?从上图表格数据可以看出, 虽然LLaMA 在MMLU这个任务上比 Chinchilla 稍差一些,但是效果也不错。这说明LLaMA在MMLU上基本也是具备涌现能力的。
其实,有个工作目前还没有看到有人做,但是这个工作是很有价值的,就是充分测试当模型变得足够小(比如10B-50B规模)以后,各种任务的涌现能力是否还具备?这是个很有价值的事情,因为如果我们的结论是即使把模型规模做小,各种任务的涌现能力可以保持,那么我们就可以放心地先追求把模型做小。
模型训练中的顿悟现象
这里介绍一个比较新的研究方向,顿悟现象,英文叫 “Grokking”。 在这里介绍模型训练过程中的顿悟,目的是希望建立起它和大模型涌现能力之间的联系,我在本文后面会尝试用顿悟现象来解释大模型的涌现能力。
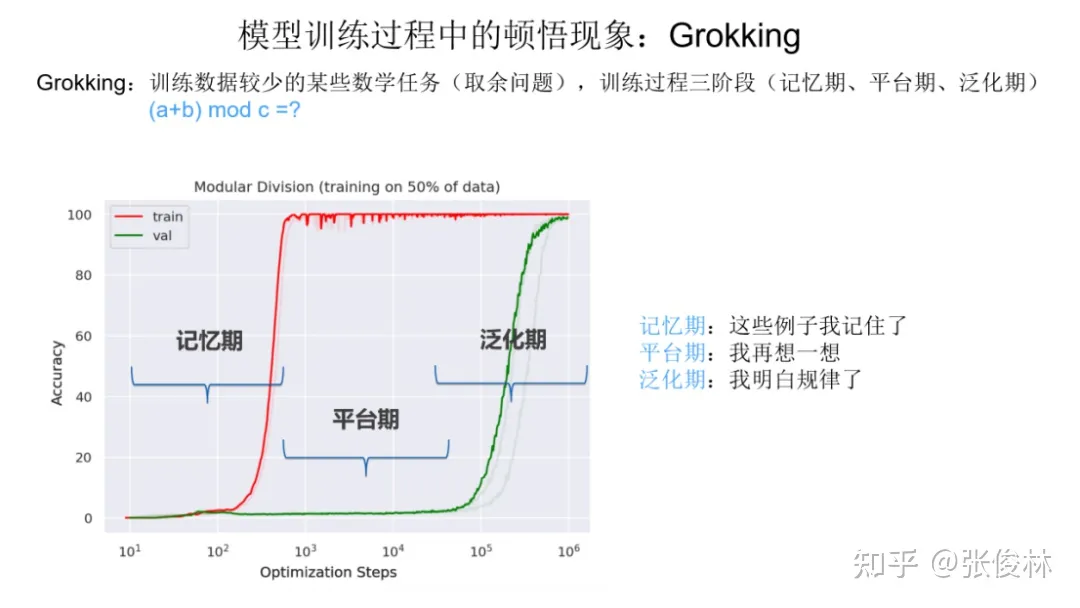
我们首先解释下什么是顿悟现象。如上图所示,对于一个训练数据较少的数学任务(通常是数字求和取余数的问题),研究人员发现一种新奇的现象。比如我们将数据集切成两块,50% 数据作为训练集(图中红线展示了随着训练过程往后走,任务指标的变化情况),50% 的数据作为验证集(图中绿线的走势展示了训练动态)。在学习数字求和取余这个任务时,它的训练动态会经历三个阶段:
- 第一个阶段是记忆期:红线对应的训练数据指标突然走高,代表模型记住了50%的训练数据的结果,而绿线对应的验证集指标接近0,说明模型完全没有泛化能力,就是说没有学会这个任务的规律。所以这个阶段模型只是在单纯地记忆训练数据。
- 第二个阶段是平台期:这个阶段是记忆期的延续,体现为验证集合效果仍然很差,说明模型仍然没有学会规律。
- 第三个阶段是泛化期:这个阶段验证集合效果突然变好,这说明突然之间,模型学会了任务里的规律,也就是我们说的,出现了顿悟现象,突然就学明白了。
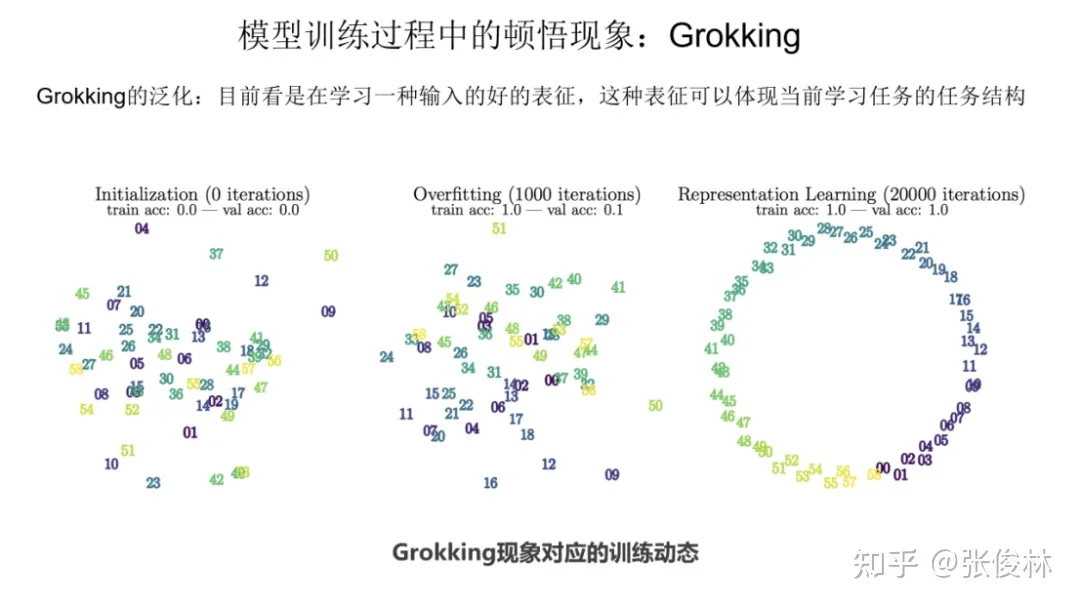
后续研究表明:Grokking 本质上是在学习输入数字的一个好的表征。如图所示,可以看到由初始化向记忆期再到顿悟现象出现的过程,数字的表征逐步开始体现当前学习任务的任务结构。
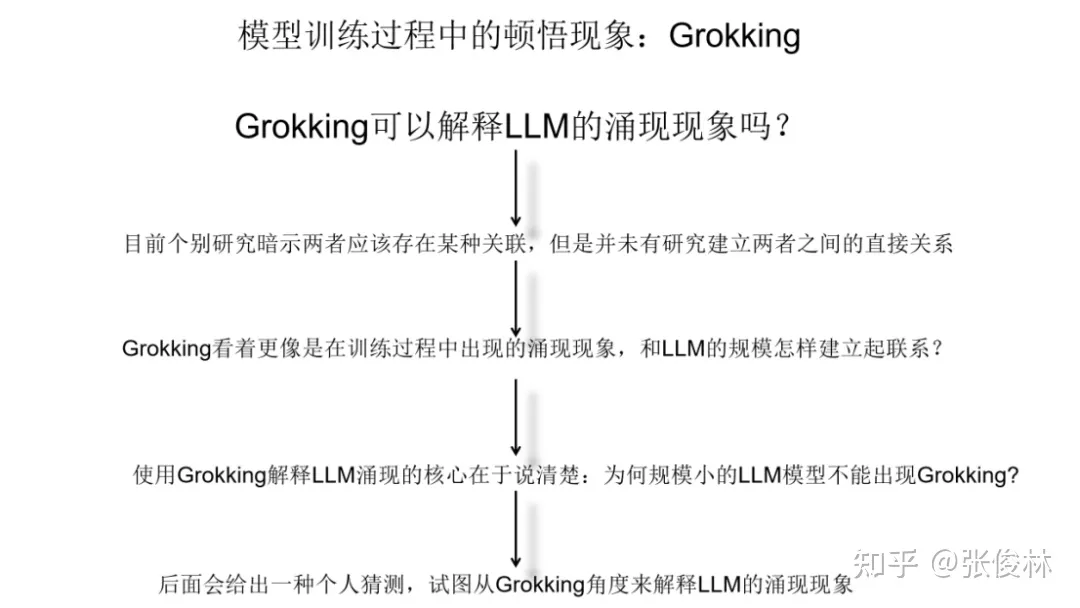
那么 ,我们能用Grokking 来解释大模型的涌现现象吗?目前,有部分研究暗示两者实际是存在某些关联的,但尚未有研究明确地指出两者之间的关系。两者从走势曲线看是非常接近的,但是有很大区别,因为Grokking描述的是模型训练动态中的表现,而涌现表达的是模型规模变化时的任务表现,虽然走势相近,但两者不是一回事。我认为,要想用Grokking解释涌现现象,核心是要解释清楚下列问题:为什么规模小的语言模型不会出现 Grokking ?这是个很关键的问题。因为如果规模小以及规模大的语言模型都会出现Grokking,那么说明Grokking和模型规模无关,也就不可能用来解释大模型的涌现现象。本文后面,我会给出一个自己的猜想,来建立两者之间的联系。
LLM 涌现能力的可能原因
为什么随着模型增大会出现涌现现象?这里给出三种猜想。前两种是现有文献提出的,第三个是我试图采用Grokking来解释涌现现象的猜想。
猜想一:任务的评价指标不够平滑
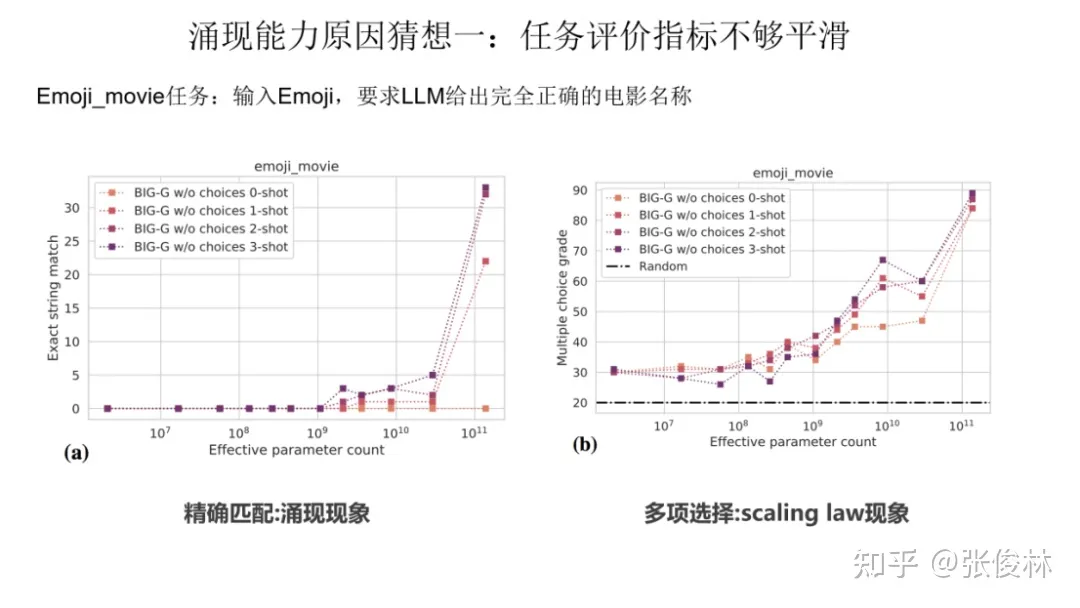
一种猜想是因为很多任务的评价指标不够平滑,导致我们现在看到的涌现现象。关于这一点,我们拿 Emoji_movie 任务来给出解释。Emoji_movie任务是说输入 Emoji图像,要求 LLM 给出完全正确的电影名称,只有一字不错才算正确,错一个单词都算错。 如上图所示,输入的Emoji是一个女孩的笑脸,后面跟着三张鱼类的图片,您可以猜猜这是什么电影。下面左侧的 2m代表 模型参数规模是 200 万参数,以及对应模型给出的回答。可以看出,随着模型规模不断增大至 128B 时,LLM才能完全猜对电影名称,但是在模型到了125m和4b的时候,其实模型已经慢慢开始接近正确答案了。
如果评价指标要求很严格,要求一字不错才算对,那么Emoji_movie任务我们就会看到涌现现象的出现,如上图图左所示。但是,如果我们把问题形式换成多选题,就是给出几个候选答案,让LLM选,那么随着模型不断增大,任务效果在持续稳定变好,但涌现现象消失,如上图图右所示。这说明评价指标不够平滑,起码是一部分任务看到涌现现象的原因。
猜想二:复杂任务 vs 子任务
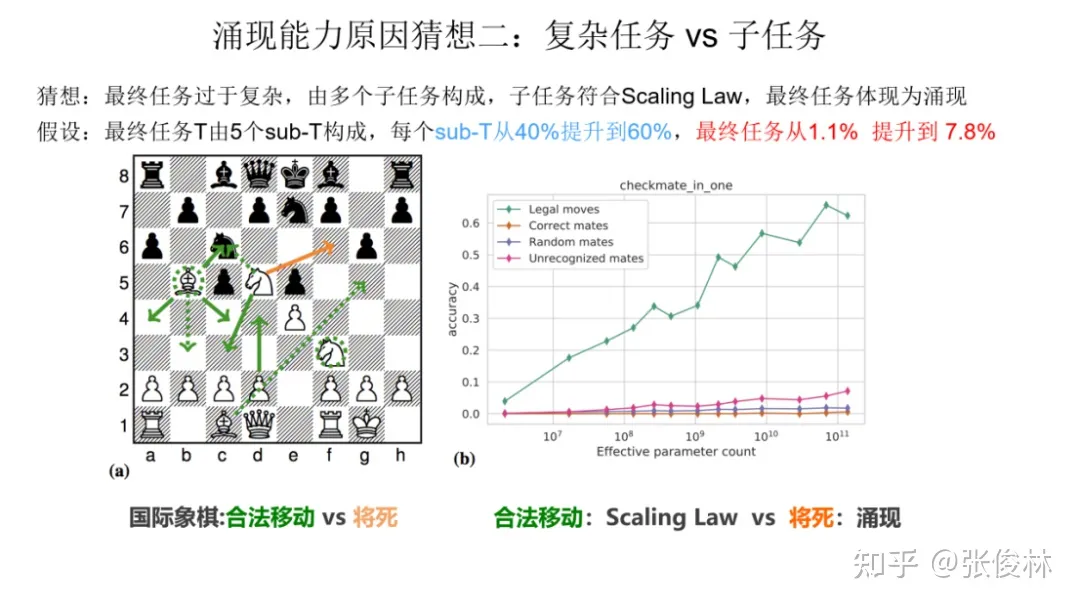
开始的时候我们提到过,展现出涌现现象的任务有一个共性,就是任务往往是由多个子任务构成的复杂任务。也就是说,最终任务过于复杂,如果仔细分析,可以看出它由多个子任务构成,这时候,子任务效果往往随着模型增大,符合 Scaling Law,而最终任务则体现为涌现现象。这个其实好理解,比如我们假设某个任务 T 有 5 个子任务 Sub-T 构成,每个 sub-T 随着模型增长,指标从 40% 提升到 60%,但是最终任务的指标只从 1.1% 提升到了 7%,也就是说宏观上看到了涌现现象,但是子任务效果其实是平滑增长的。
我们拿下国际象棋任务来作为例子,如上图所示,让语言模型预测下一步,最终评价指标是只有“将”死才算赢。如果按“将死”评估(红线),发现随着模型增大,模型在缓慢上升,符合涌现的表现。若评估LLM合法移动(绿线),而在合法的移动步骤里进行正确选择才够最后“将死”是个子任务,所以其实这是比将死简单的一个子任务。我们看合法移动随着模型规模,效果持续上升。此时,我们是看不到涌现现象的。
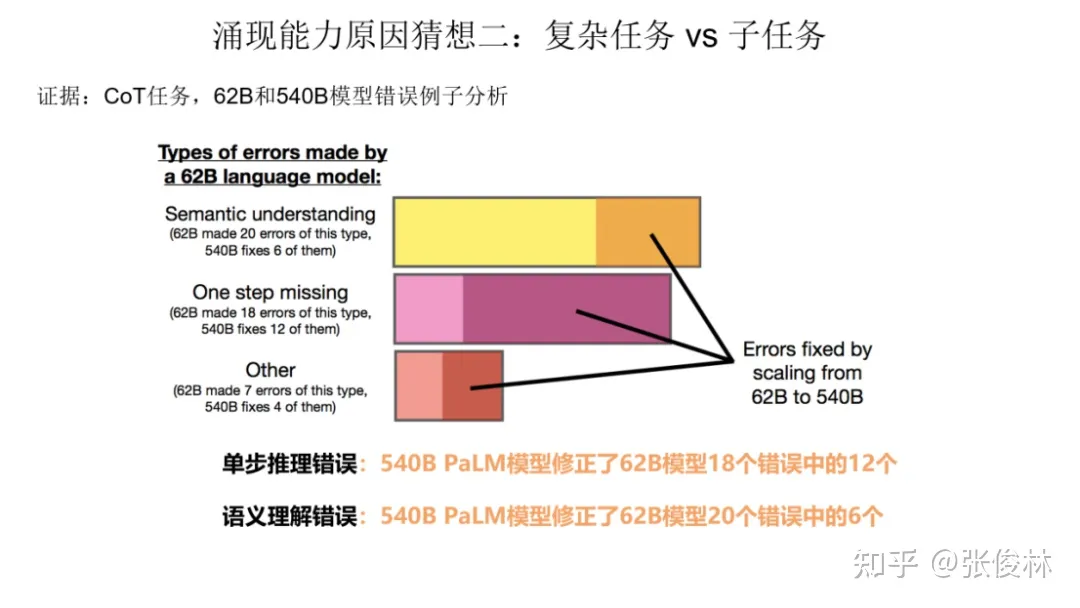
这里可以给出一个例证,如上图所示,对于CoT 任务,谷歌用 62B 和 540B 模型对LLM做错的例子进行了错误分析。对于62B做错、而540B做对的例子分析,可以看出,最多的一类错误来自于单步推理错误,这其实也能侧面说明复杂任务和子任务的关系。
猜想三:用 Grokking 来解释涌现
这里介绍我设想的如何用Grokking来解释涌现现象的一种猜想,在建立两者之间关系前,我们先来看两个已知的事实,然后在事实基础上作出推论。
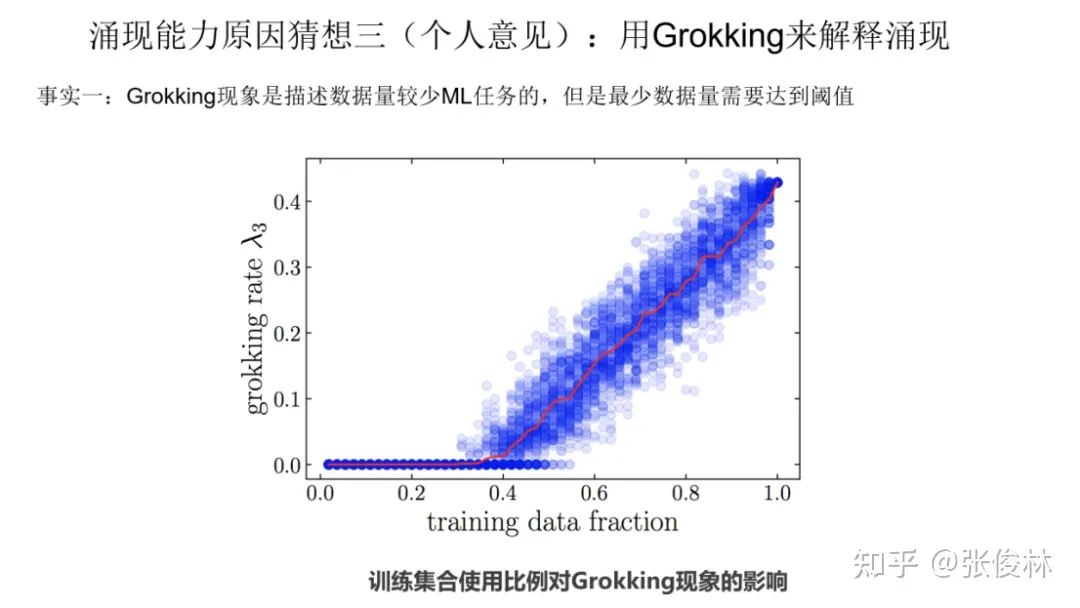
首先,第一个事实是 Grokking 现象是描述训练数据量较少的 ML 任务的,但是任务最小训练数据量必须达到一定的量,才会出现 Grokking 现象。这里有两点,一个是本身训练数据量少,另外是最小数据量要达到临界值。只有同时满足上面两个条件,才有可能出现Grokking现象。上图的意思是:当我们只拿40%及以下比例的数据来训练模型的时候,我们看不到Grokking现象,只有记忆没有泛化,只有最小训练数据比例超过40%,才会出现模型的顿悟。这是一个已被验证的事实。
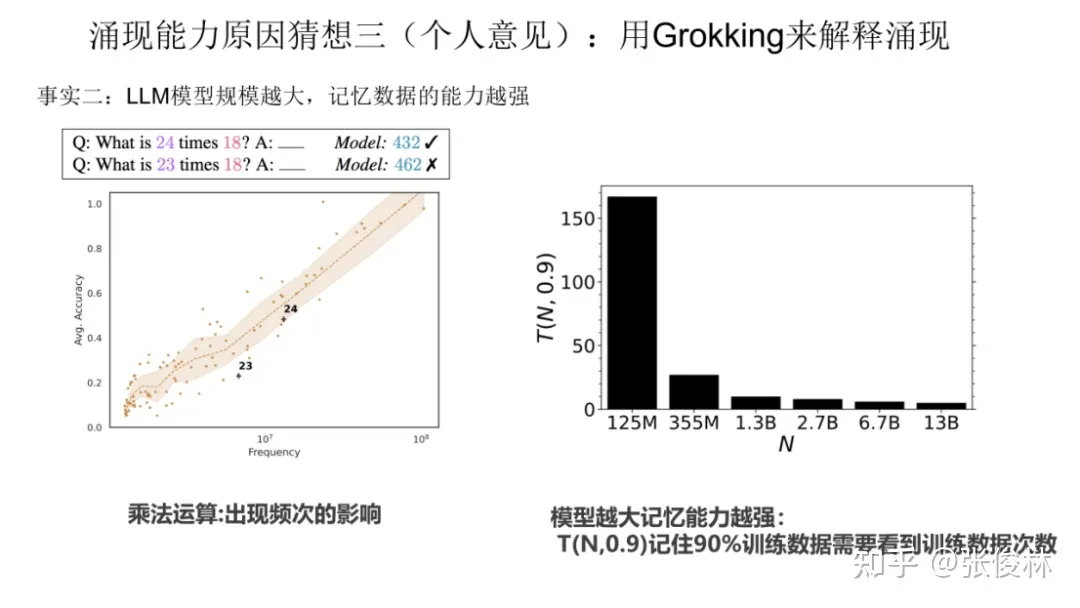
第二个事实是 LLM 模型规模越大,记忆数据的能力越强。关于这点目前有很多研究已经可以证明,如果简单理解的话,可以理解为:对于某个任务T,假设预训练数据里包含与任务T相关的训练数据量有100条,那么大模型可以记住其中的70条,而小模型可能只能记住30条。虽不精确,但大概是这个意思。
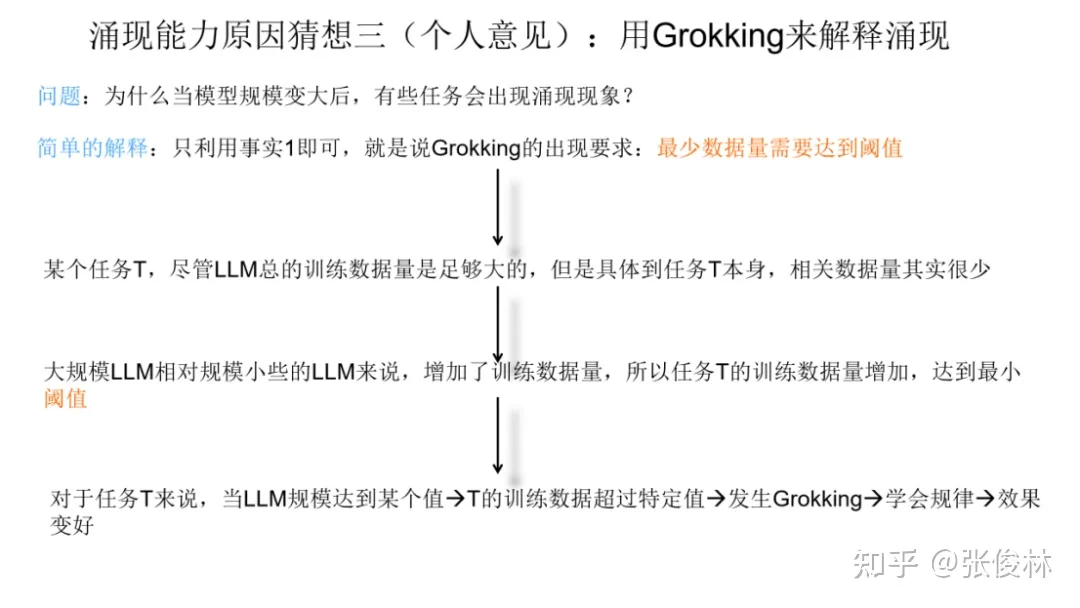
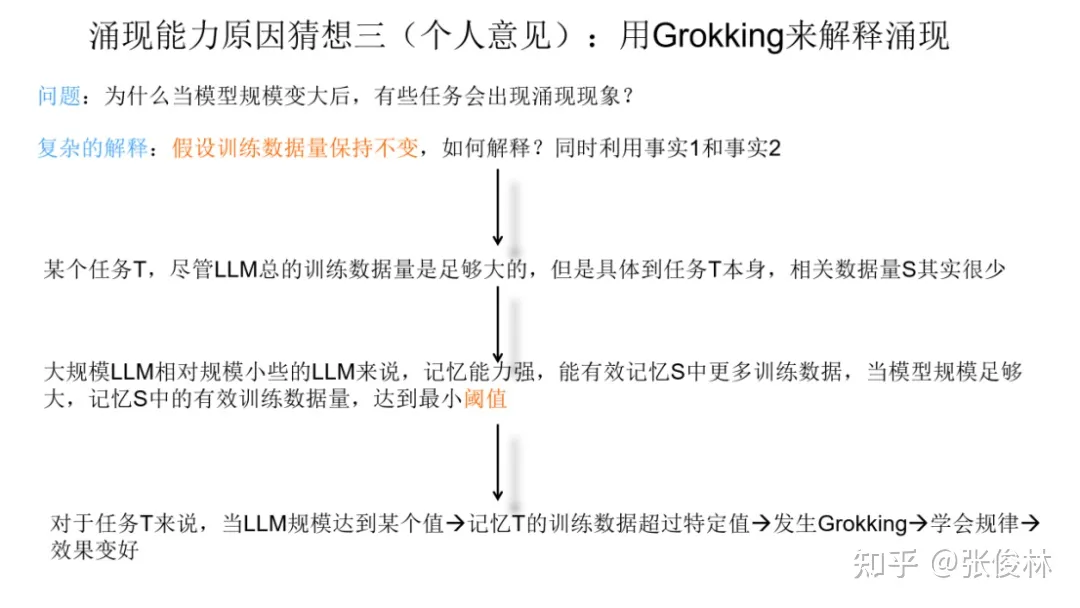
在上面的两个事实基础上,我们试图来用Grokking解释大模型的涌现现象。首先我们给出一个简单的解释,这个解释只需要利用第一个事实即可,就是说,任务的最少训练数据量需要达到临界值,才会出现Grokking。在这个事实下,对于某个任务T,尽管我们看到的预训练数据总量是巨大的,但是与T相关的训练数据其实数量很少。当我们推大模型规模的时候,往往会伴随着增加预训练数据的数据量操作,这样,当模型规模达到某个点的时候,与任务T相关的数据量,突然就达到了最小要求临界点,于是我们就看到了这个任务产生了Grokking现象。在语言模型的宏观角度,看起来就是模型达到了某个规模,突然任务T效果就开始变好,而模型规模较小的时候,因为没有达到临界值,所以一直没有Grokking现象,看起来就是语言模型没有这个能力。这是一种可以从Grokking角度解释大模型涌现现象的可能。
上面这个猜想其实有个约束条件,因为我们有个假设,说随着模型规模增大,训练数据量也在增大。如果这个假设不存在,也就是说,随着模型规模增大,我们固定住训练数据量不变。那么,这种情况下,怎么能用Grokking解释涌现现象呢?此时如果我们同时利用事实1和事实2,也可以给出一个解释。更具体来说,我们假设在预训练数据中,某个任务T有 100 个训练数据,当模型规模小的时可能只记得 30 个,达不到Grokking现象的临界点,而当模型规模推大时,因为模型记忆能力增强,可能就能记住其中的50个,这意味着它可能超过了Grokking的临界点,于是会出现 Grokking 里面的泛化现象。如果从这个角度看,其实我们也可以从Grokking角度来解释为何只有大模型才会具备涌现现象。
猜想四: 分歧点问题
这篇文章给了我很大的启发,说一下我个人对LLM中涌现和Grokking现象的一点想法。
我曾用蓝眼睛岛问题来测试GPT4的逻辑推理能力,并发现了一些有趣的现象:
事实1:ChatGPT知道蓝眼睛岛问题,但不能完全正确地说出问题的内容,并且完全无法解决问题,给出的推理过程乱七八糟。这说明ChatGPT并没有完全记住蓝眼睛岛问题。
事实2:GPT4能说出问题的内容,并且能给出像标准答案一样的推理过程(多次测试正确率100%)。这说明GPT4完全记住了蓝眼睛岛问题及其推理过程。
事实3:当我将原问题的内容修改为“外来者说至少有10个居民的眼睛是蓝色的”,GPT4立即就傻了(10次测试,使用不同的prompt,正确率0%)。但从GPT4回答的内容可以看出,它其实知道应该怎样推理,只是会把推理过程往原问题的推理上靠。甚至在完全正确的推理过程中,修改一个数字,强行得出原问题的结果。这说明GPT4对蓝眼睛岛问题已经过拟合了。
事实4:我将问题中的“蓝眼睛岛”换成“绿眼睛村”,别的内容不变,GPT4依然会把推理过程往原问题的推理过程上靠,但这一次没有在推理正确的情况下,强行修改一个数字来得到原问题的结果了。(5次测试,正确1次,正确率20%)
事实5:我重新构造了这个问题,改为:“在一场实验中,实验者通过计算机模拟了一些具有推理能力的智能体,这些智能体分成A、B两类。智能体之间不能相互交流,每个智能体都知道剩余的智能体的数量和剩余的所有智能体的类别,但不知道自己的类别。规则是,每一分钟对所有智能体进行一次检查,一旦发现有智能体知道了自己的类别,这个智能体就会被消灭。 有一天,实验者向所有智能体宣布:至少有10个智能体是A类的。问题是,如果有N个A类智能体(N>10),将会发生什么?”问题的表述完全不同了,但推理过程本质上是相同的。这一次GPT4成功给出了正确的推理过程和结果(10次测试,正确率70%)。这说明GPT4其实已经掌握了推理方法,并不只是记下了蓝眼睛岛的推理过程。
通常来说,我们认为过拟合发生在模型对训练数据的特征学习过于深入,以至于捕捉到了数据中的噪声和随机波动。但我认为,对于LLM来说,完全记住训练数据中的内容与掌握相关规律并不矛盾。就像在前面的事实3-事实5中,GPT4表现出了对蓝眼睛岛问题的过拟合,同时又掌握了推理方法。
然而,不矛盾并不意味着不会相互干扰。因为GPT4是根据上文来预测下一个token的概率,而修改后的蓝眼睛岛问题跟原问题只有一个数字的差别,所以我猜想,在推理过程中,由于记忆的干扰,会出现许多个“分歧点”。(“分歧点”是我在跟GPT4聊天的时候想到的一个概念,我不清楚是否已经存在类似的概念。它的意思是,在这一个token的不同选择,会产生完全不同的后续内容。举一个例子,上文输入“太阳能是一种”,输出的三个候选词分别是“可再生的”、“环保的”、“高效的”,由于GPT4是用Top-P Sampling随机采样的,于是后面的输出内容就会因为对候选词随机采样结果的不同而完全不同,这就是一个分歧点。)这些分歧点有的候选词导向正确的推理过程,有的候选词导向原蓝眼睛岛问题的记忆。即使后者的概率很小,多个分歧点叠加起来后出错的概率也会大大增加。
这也是为什么在事实3中GPT4在推理过程中会用各种方式往原问题的推理过程上靠,而在我将“蓝眼睛岛”换成“绿眼睛村”以及重新构造这个问题后,GPT4的表现会变好的原因。因为原问题的记忆产生的干扰减小了,分歧点变少了。
我猜想在LLM中的涌现和Grokking现象,也是类似的情况。在“平台期”(或模型不够大时),模型可能已经掌握了任务T的规律,但对任务T训练数据的记忆或之前无监督预训练时学到的候选词导致了分歧点,干扰了模型输出的表现。随着任务T的训练数据的增加(或模型的增大),导向正确结果的候选词概率随之变大,导向错误结果的候选词概率变小,直到某一刻,它们突然不再成为候选词,于是分歧点减少,模型输出正确结果的概率迅速上升。
要验证这个猜想,可以考虑在分歧点用蒙特卡洛树搜索方法,对每个候选词用GPT4生成后续文本,然后使用人类反馈强化学习中训练的那个价值网络或别的方式进行评分(或者更简单地,降低P值或temperature值,使模型输出更加稳定),看能否提高模型泛化能力,或看随着模型的增大,任务T的评分是否符合Scaling Law。